Repaso de áreas de polígonos regulares y no regulares

 Estas son las fórmulas que debemos memorizar para hallar las áreas de las figuras geométricas elementales que hemos  visto.

Démonos tener en cuento los elementos básicos que quedan reflejadas en ellas:

• Lados de un polígono. son el conjunto de  segmentos   comprendidos entre los vértices de un polígono, que conforman el perímetro de la figura poligonal.

• Vértices de un polígono:  punto de unión entre dos lados consecutivos,

• Perímetro: suma de los lados de un polígono.

• Circunferencia: línea que rodea a un círculo. 

• Diagonal del polígono: son los segmentos que une  dos vértices no  consecutivos de un polígono.

• Radio: es la línea recta que une el punto central de una circunferencia y cualquiera de los puntos de la circunferencia.

• Apotema: es la perpendicular  entre el centro de la figura y cualquiera de sus lados.

Ejemplos de estas definiciones en imágenes:

                                                       Elementos de una circunferencia.

Para hallar el área de una figura poligonal irregular podremos ver las áreas de las figuras regulares que están en ella y sumarlas.

 

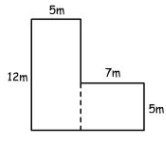
En esta figura podemos buscar su área del siguiente modo: 

1. Hallo el área del rectángulo vertical   12m x  5m  =   60 ㎡
2. Hallo el área del rectángulo horizontal  7 m x 5 m =  35 ㎡
3. Sumo ambos   60 ㎡  +  35 ㎡  = 95 ㎡

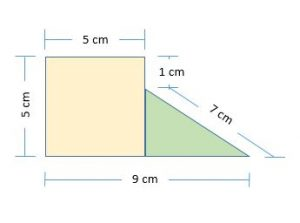
Otro ejemplo:

1. Hallamos el área del cuadrado 5cm x 5 cm = 25 ㎠
2. Hallamos el área del triangulo base (9 cm-5cm = 4 cm)  y altura (5cm  -1 cm = 4 cm) . Sería 4x4 dividido entre 2  total 8 ㎠.
3. Súmanos ambas áreas  25 ㎠ +8 ㎠ =  33 ㎠